فروش ویژه سرور اختصاصی
الگوریتم هایی که هر برنامه نویسی باید بداند

- خرداد 17, 1402
- 0
- ملیحه ایزی
در برنامه نویسی، الگوریتم مجموعه ای از دستورالعمل ها یا رویه ای برای حل یک مسئله خاص یا دستیابی به یک کار خاص است. الگوریتمها را میتوان در هر زبان برنامهنویسی بیان کرد و میتواند به سادگی یک توالی از عملیات اصلی یا به پیچیدگی یک فرآیند چند مرحلهای شامل ساختارهای داده و منطق مختلف باشد. هدف اصلی یک الگوریتم دریافت ورودی، پردازش آن و ارائه خروجی مورد انتظار است. الگوریتم ها را می توان بر اساس پیچیدگی زمانی و مکانی، تکنیک مورد استفاده برای حل مسئله و نوع مسئله ای که حل می کند طبقه بندی کرد. نمونههایی از الگوریتمها عبارتند از مرتبسازی، جستجو، پیمایش نمودار، دستکاری رشتهها، عملیات ریاضی و بسیاری موارد دیگر.
الگوریتم هایی که در مورد آنها صحبت خواهیم کرد:
الگوریتم های مرتب سازی: مرتب سازی یک عملیات اساسی در علوم کامپیوتر است و چندین الگوریتم کارآمد مانند مرتب سازی سریع، مرتب سازی ادغامی و مرتب سازی هرمی برای آن وجود دارد.
الگوریتم های جستجو: جستجوی یک عنصر در یک مجموعه داده بزرگ یک کار رایج است و چندین الگوریتم کارآمد مانند جستجوی باینری و جداول هش برای آن وجود دارد.
الگوریتم های گراف: الگوریتم های نمودار برای حل مسائل مربوط به گراف ها استفاده می شود، مانند یافتن کوتاه ترین مسیر بین دو گره یا تعیین اینکه آیا یک گراف متصل است یا خیر.
برنامه نویسی پویا: برنامه نویسی پویا تکنیکی است برای حل مسائل از طریق تجزیه آنها به مسائل فرعی کوچکتر و ذخیره راه حل های این مسائل فرعی برای جلوگیری از محاسبات اضافی.
الگوریتمهای حریصانه: الگوریتمهای حریص برای حل مسائل بهینهسازی با انتخاب بهینه محلی در هر مرحله با امید به یافتن بهینه جهانی استفاده میشوند.
الگوریتم تقسیم و حل(Divide and Conquer: (Divide and Conquer یک الگوریتم طراحی الگوریتم مبتنی بر بازگشت چند شاخه ای است. الگوریتم تقسیم و غلبه یک مسئله را به مسائل فرعی از نوع مشابه یا مرتبط تقسیم می کند، تا زمانی که این مسائل به اندازه کافی ساده شوند که مستقیماً حل شوند.
Backtracking : Backtracking یک تکنیک الگوریتمی کلی است که جستجوی هر ترکیب ممکن را به شیوه ای سیستماتیک در نظر می گیرد و به محض اینکه تشخیص داد که نمی تواند بخشی از راه حل باشد، مسیر خاصی را رها می کند.
الگوریتم تصادفی: الگوریتم های تصادفی از تصادفی بودن برای حل یک مسئله استفاده می کنند. می تواند برای حل مسائلی که نمی توانند به طور قطعی حل شوند یا برای بهبود میانگین پیچیدگی موردی یک مسئله مفید باشد.
این الگوریتم ها به طور گسترده در برنامه های مختلف مورد استفاده قرار می گیرند و برای یک برنامه نویس مهم است که درک قوی از آنها داشته باشد. بنابراین تمام تلاشم را خواهم کرد تا آنها را توضیح دهم.
1.الگوریتم های مرتب سازی
مرتب سازی سریع (Quicksort)
Quicksort یک الگوریتم تقسیم و غلبه است که یک عنصر “pivot” را از آرایه انتخاب می کند و سایر عناصر را با توجه به کوچکتر یا بزرگتر بودن آنها به دو آرایه فرعی تقسیم می کند. سپس آرایه های فرعی به صورت بازگشتی مرتب می شوند.

در تصویر زیر یک آرایه نمونه می بینیم که به روش مرتب سازی سریع مرتب شده است.
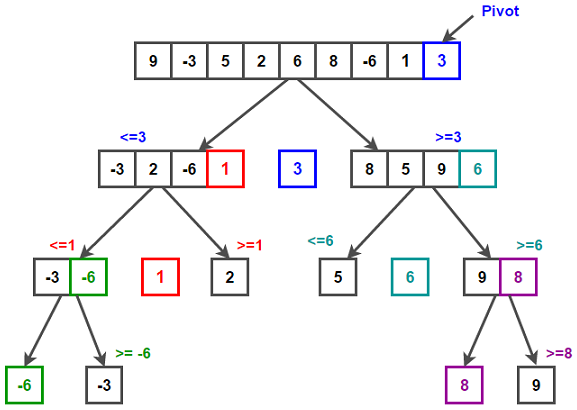
عنصر pivot می تواند هر کدام از عناصر آرایه باشد:
- عنصر اول بعنوان عنصر pivot انتخاب شود
- عنصر انتهای آرایه بعنوان عنصر pivot انتخاب شود
- عنصر میانی بعنوان عنصر pivot انتخاب شود
- …
در نمونه بالا عنصر انتهایی بعنوان عنصر pivot انتخاب شده است. همه مقادیر کمتر از این عنصر در آرایه سمت چپ و مقادیر بیشتر از این در آرایه سمت راست قرار می گیرد. سپس در دو آرایه جدید عنصر pivot جدید را تعریف می کنیم و این روال را تا انتها انجام میدهیم سپس بصورت بازگشتی آرایه را بصورت مرتب شده از چپ ترین حالت بازنویسی می کنیم.
مرتب سازی ادغامی(mergesort)
الگوریتم مرتب سازی ادغامی یک الگوریتم تقسیم و غلبه است که یک آرایه را به دو قسمت تقسیم می کند، دو نیمه را مرتب می کند و سپس آنها را دوباره با هم ادغام می کند.

در تصویر زیر یک آرایه نمونه می بینیم که به روش مرتب سازی ادغامی مرتب شده است.
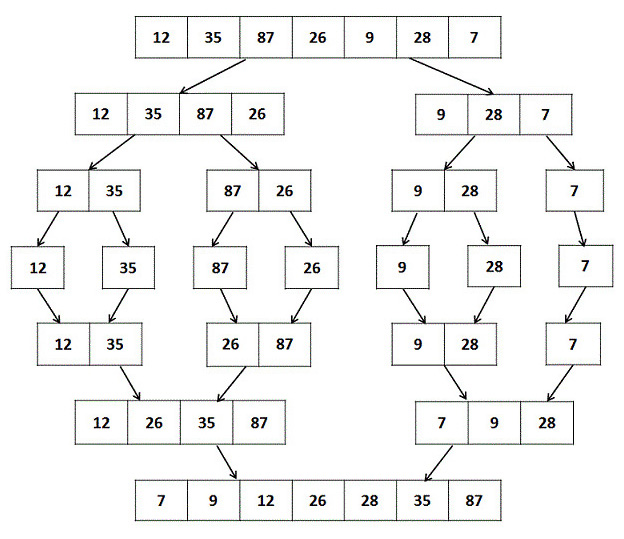
آرایه را به دو بخش تقریبا برابر تقسیم می کنیم و سپس آرایه های موجود را تقسیم می کنیم. این تکرار تا زمانی که به یک آرایه یک عضوی برسیم ادامه پیدا می کند سپس مرتب سازی انجام و آرایه ها با هم ادام می شوند.
مرتبسازی هرمی (Heap Sort)
الگوریتم مرتبسازی پشته یک الگوریتم مرتبسازی مبتنی بر مقایسه است که یک پشته از عناصر ورودی میسازد و سپس به طور مکرر حداکثر عنصر را از پشته استخراج میکند و آن را در انتهای آرایه خروجی مرتبشده قرار میدهد.
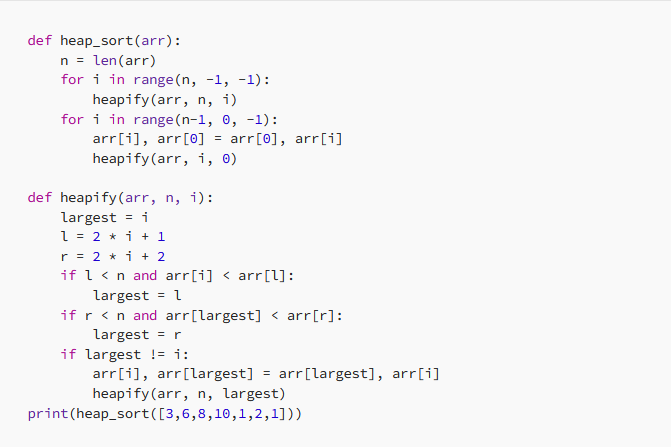
بر اساس تعریف درخت heap، در یک max-heap (یا min-heap) بزرگترین (یا کوچکترین) مقدار بین دادهها همواره در ریشه درخت قرار دارد. مراحل مرتبسازی هرمی min-heap به ترتیب زیر خواهد بود:
Step 0 ) min-heap: 1, 4, 5, 8, 6, 9 – list
Step 1 ) min-heap: 4, 6, 5, 8, 9 – list: 1
Step 2 ) min-heap: 5, 6, 9, 8 – list: 1, 4
Step 3 ) min-heap: 6, 8, 9 – list: 1, 4, 5
Step 4 ) min-heap: 8, 9 – list: 1, 4, 5, 6
Step 5 ) min-heap: 9 – list: 1, 4, 5, 6, 8
Step 6 ) min-heap: – list: 1, 4, 5, 6, 8, 9
در پایان، آرایه list شامل اطلاعات مرتبشده صعودی است.
2. الگوریتم های جستجو
جستجوی دودویی (Binary Search)
جستجوی باینری یک الگوریتم کارآمد برای یافتن یک آیتم از لیست مرتب شده اقلام است. با تقسیم مکرر به نصف بخشی از آرایه مورد جستجو تا زمانی که مقدار هدف پیدا شود، کار می کند. در جستجوی دودویی، جستجو در یک آرایه مرتب شده انجام می شود.

در آرایه موجود در تصویر زیر بدنبال عدد50می گردیم.
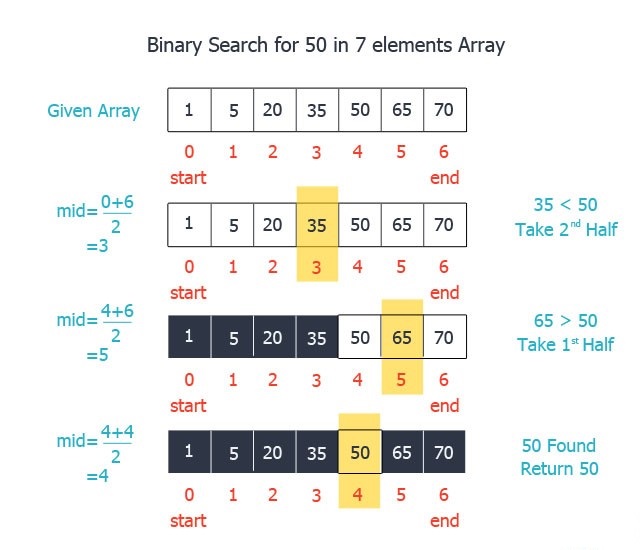 در مرحله اول عدد موردجستجو با عنصر میانی آرایه مقایسه می شود. اگر برابر بود که اندیس آرایه برمیگردد در غیراینصورت اگر عدد ما بزرگتر از عنصر میانی بود بدنیال این عدد در سمت راست و در غیرایصورت در سمت چپ آرایه به جستجو می پردازیم. سپس همین مراحل را تا پیدا کردن عدد مدنظرمان انجام می دهیم.
در مرحله اول عدد موردجستجو با عنصر میانی آرایه مقایسه می شود. اگر برابر بود که اندیس آرایه برمیگردد در غیراینصورت اگر عدد ما بزرگتر از عنصر میانی بود بدنیال این عدد در سمت راست و در غیرایصورت در سمت چپ آرایه به جستجو می پردازیم. سپس همین مراحل را تا پیدا کردن عدد مدنظرمان انجام می دهیم.
جداول هش(Hash Tables)
یک جدول هش ساختار داده ای است که کلیدها را به مقادیر نگاشت می کند، با استفاده از یک تابع هش برای محاسبه شاخص در آرایه ای از سطل ها یا شکاف ها، که از آنها می توان مقدار مورد نظر را پیدا کرد.

3. الگوریتم گراف
الگوریتم کوتاهترین مسیر دایجسترا(Dijkstra)
الگوریتمی برای یافتن کوتاهترین مسیر بین گرهها در یک گراف است.
گراف وزن دار
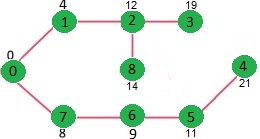
گراف وزن دار، گرافی است که یالهای آن دارای وزن یا هزینه هستند. وزن هر یال میتواند نشان دهندهی فاصله، زمان یا هر چیزی که در آن مدل، دو نود را به هم متصل میکند باشد. به عنوان مثال در گراف وزن دار زیر شمارههای با رنگ مشکی روی هر یال نمایشگر وزن آن یال است.
گراف زیر را درنظر بگیرید میخواهیم به کمک الگوریتم دایجسترا با شروع از گره 0 همه گره ها را بازدید کنیم.
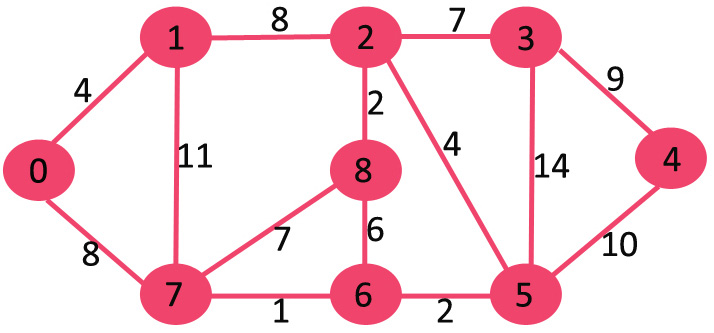
از گره صفر شروع می کنیم و گره های مسیرهای با وزن کمتر را بازدید می کنیم. گره صفر به یک با وزن 4 و به 7 با وزن 8 است پس گره 1 بازدید می شود.
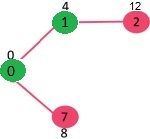
برای رسیدن به گره 2 وزن12 و گره 7 وزن 8 را داریم پس گره 7 بازدید می شود.
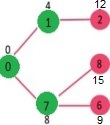
طبق قاعده توضیح داده شده در بالا سپس گره 6 بازدید می شود.
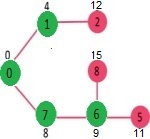
به همین روال تا انتها ادامه میدهیم تا تمامی گره ها یکبار بازدید شوند.
در زیر کدهای الگوریتم دایجسترا را می توانیم مشاهده کنیم.

4. برنامه نویسی پویا
دنباله فیبونانچی
یک مثال کلاسیک از مسئله ای که با استفاده از برنامه نویسی پویا قابل حل است، دنباله فیبوناچی است.
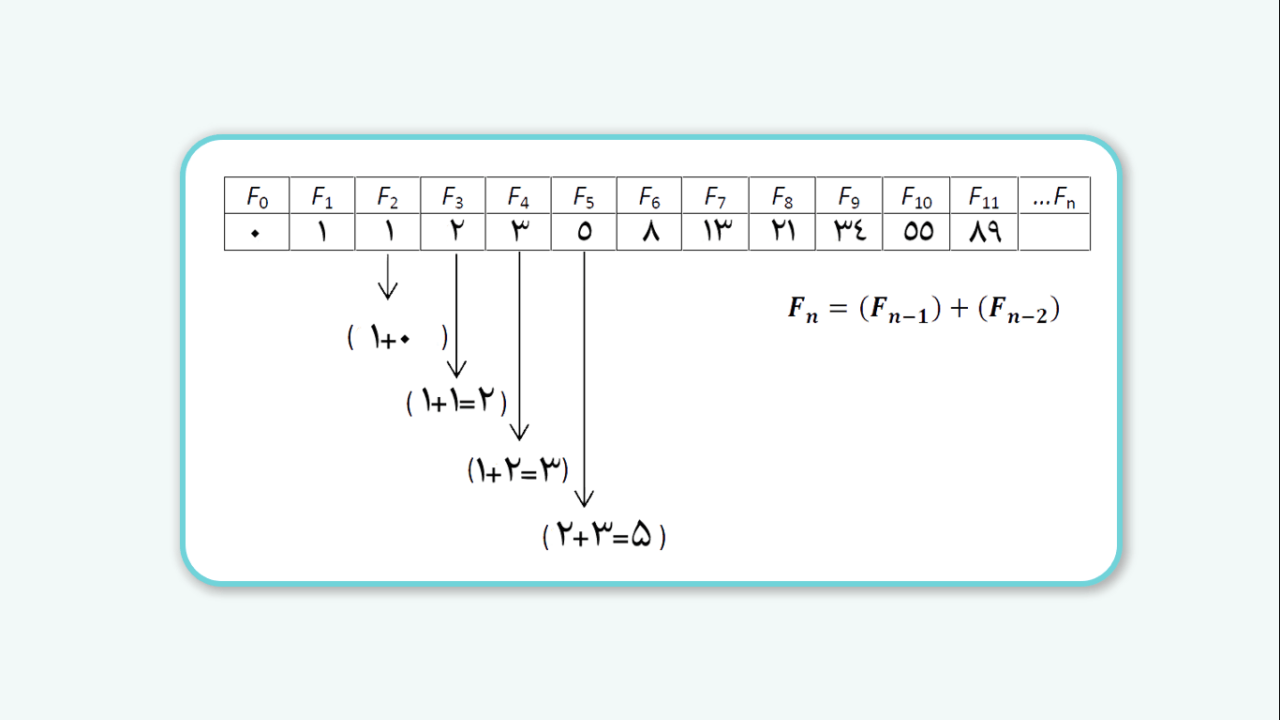
سری فیبونانچی که شهرتش تنها به این دلیل نیست که هر جمله با مجموع دو جملهی پیشین خود برابری میکند، بلکه به این دلیل است که خارجقسمت هر دو جملهی کنار هم خاصیت حیرتانگیزی نزدیک به عدد ۱.۶۱۸ را دارد که به «نسبت طلایی» مشهور است. بهعنوانمثال تقسیم ۸۹ بر ۵۵ یا ۱۴۴ بر ۸۹ یا ۲۳۳ بر ۱۴۴ همگی برابر با ۱.۶۱۸ میشود.

5. الگوریتم های حریصانه
کدگذاری هافمن
کدگذاری هافمن یک الگوریتم فشرده سازی داده های بدون تلفات است که از یک الگوریتم حریص برای ساخت یک کد پیشوند برای مجموعه معینی از نمادها استفاده می کند.
فرض کنید تعداد تکرارهای یک رشته مطابق مثال زیر باشد حال بیاید کدگذاری هافمن را بر روی آن پیاده سازی کنیم.

حال با کاراکترهایی که کمترین تکرار را دارند شروع می کنیم و آنها را با هم ادغام کن و گره جدید ایجاد کن
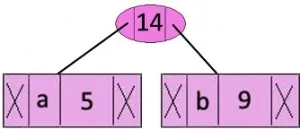
در ادامه باز دو گره با کمترین تکرار را از درخت کمینه مجدد استخراج کنید و سپس این مورد را تا انتها ادامه میدهیم.
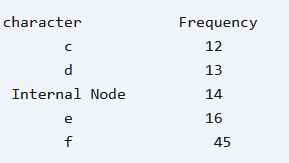
در اینجا cو d را ادغام می کنیم.
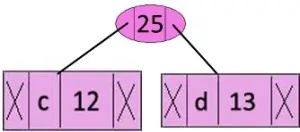
درخت کمینه تا انتها به شکل زیر تشکیل می شود و سپس یالهای سمت راست را عدد1 و یالهای سمت چپ را وزن صفر قرار می دهیم.
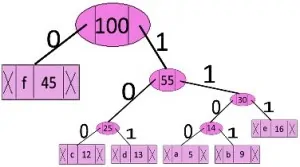
و در نتیجه کدها بصورت زیر از سمت ریشه به سمت برگها نوشته می شود.

کدهای این الگوریتم بصورت زیر است.

6. بازگشتی
مسئله N-Queens
مسئله N-Queens یک مسئله کلاسیک است که می توان آن را با روش های متفاوتی حل کرد یکی از آن روش ها استفاده از Backtracking حل کرد. هدف قرار دادن N وزیر در صفحه شطرنج NxN به گونه ای است که هیچ وزیری نتواند به وزیر دیگری حمله کند.

این الگوریتم شروع به قرار دادن وزیرها در ردیف اول می کند و برای هر وزیر قرار داده شده بررسی می کند که آیا مورد حمله وزیر قبلی قرار گرفته است یا خیر. اگر نه، به ردیف بعدی می رود و روند را تکرار می کند. اگر یک وزیر در موقعیتی قرار گیرد که در معرض حمله باشد، الگوریتم به عقب برمیگردد و موقعیت دیگری را امتحان میکند. این کار تا زمانی ادامه می یابد که تمام وزیرها بدون حمله به یکدیگر بر روی صفحه قرار گیرند.
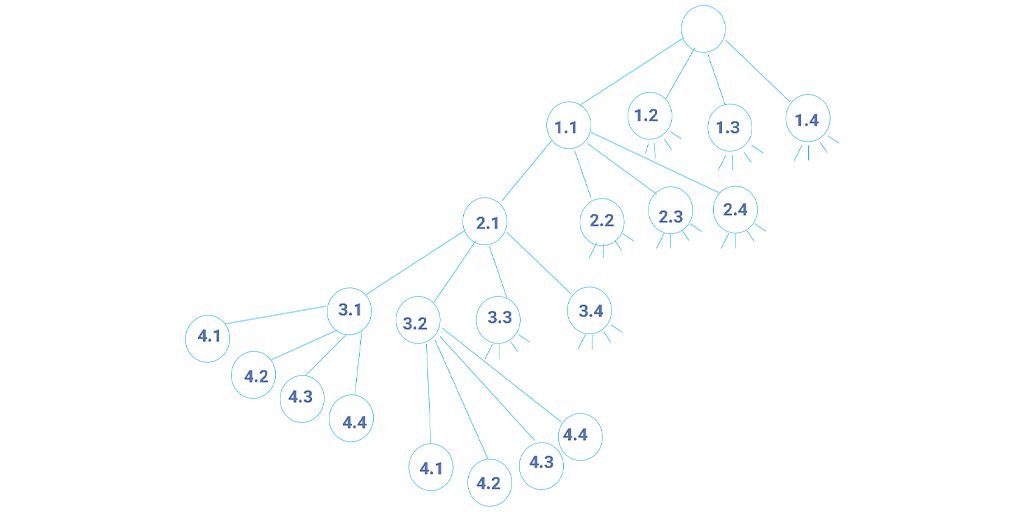
شکل بالا درخت تمام حالاتی است که 4 وزیر را میتوان در صفحه شطرنج 4 در 4 قرار داد. وزیر اول میتواند در ستونهای 1 تا 4 قرار گیرد. وزیر دوم هم میتواند در سطر دوم در ستونهای 1 تا 4 قرار بگیرد و همین طور الی آخر ادامه دارد. حالا برای پیدا کردن جواب از درخت باید درخت را پیمایش کنیم. ابتدا یک حالت را با پیمایش عمقی درخت بهدست میآوریم.
7. الگوریتم تصادفی شده
الگوریتم تصادفی تکنیکی است که از منبع تصادفی به عنوان بخشی از منطق خود استفاده می کند. معمولاً برای کاهش زمان اجرا یا پیچیدگی زمانی و یا حافظه استفاده شده یا پیچیدگی فضا در یک الگوریتم استاندارد استفاده می شود. این الگوریتم با تولید یک عدد تصادفی rr در محدوده مشخصی از اعداد و تصمیم گیری بر اساس مقدار rr کار می کند.
یک الگوریتم تصادفی میتواند با برگرداندن یک سکه یا کشیدن یک کارت به منظور تصمیمگیری، در شرایط شک کمک کند. به طور مشابه، این نوع الگوریتم میتواند با نمونهبرداری تصادفی از ورودی به سرعت بخشیدن به فرآیند brute force کمک کند تا راهحلی به دست آید که ممکن است کاملاً بهینه نباشد، اما برای اهداف مشخص شده به اندازه کافی خوب باشد.
الگوریتم های تصادفی معمولاً به یکی از دو شکل رایج طراحی می شوند: به عنوان الگوریتم لاس وگاس یا به عنوان الگوریتم مونت کارلو. الگوریتم لاس وگاس در مدت زمان مشخصی اجرا می شود. اگر در آن بازه زمانی راه حلی پیدا کند، راه حل دقیقاً درست خواهد بود. اما ممکن است زمان آن تمام شود و راه حلی پیدا نکند. از سوی دیگر، الگوریتم مونت کارلو یک الگوریتم احتمالی است که بسته به ورودی، احتمال کمی دارد که نتیجه نادرست ایجاد کند یا به طور کلی نتیجه ای تولید نکند.
– مرتب سازی سریع تصادفی: نوعی از الگوریتم مرتب سازی سریع که در آن محور به طور تصادفی انتخاب می شود.

اینها برخی از رایج ترین الگوریتم هایی هستند که هر برنامه نویسی باید با آنها آشنا باشد. درک این الگوریتم ها و اجرای آنها می تواند به برنامه نویس کمک کند تا در طراحی و اجرای راه حل های کارآمد تصمیمات بهتری بگیرد.
تمامی حقوق برای ماکرونت محفوظ است.