فروش ویژه سرور اختصاصی
10 کاربرد عملی درخت باینری
- مرداد 2, 1401
- 0
- ملیحه ایزی
چرا ساختارهای داده ای اهمیت دارند ؟
ما امروزه در دنیایی قرار گرفته ایم که توسط داده ها احاطه شده ایم از پست های شبکه های اجتماعی بگیرید تا دوستان آشنایان و همه اطلاعاتی که در اینترنت ذخیره می کنید در واقع داده هایی هستند که متعلق به شماست. برای اینکه برنامه نویسان بتوانند نرم افزارهای کارآمدتری طراحی کنند نیاز است تا داده ها را به شیوه ای ساختار یافته نمایند. از آنجا که داده حیاتیترین موجودیت در علم کامپیوتر است، ارزش واقعی ساختمان دادهها را مشخص می کند.
ساختار داده درختی چیست و چرا از آن استفاده می کنیم؟
هنگامی که به یک ساختار داده درختی اشاره می شود، منظور یک نوع غیر خطی از ساختار داده است که داده ها را به شیوه ای سلسله مراتبی سازماندهی می کند، متشکل از نودها که توسط یالها به هم متصل می شوند. هر نود یا گره دارای یک مقدار است و گاهی اوقات می تواند فرزند داشته باشد.
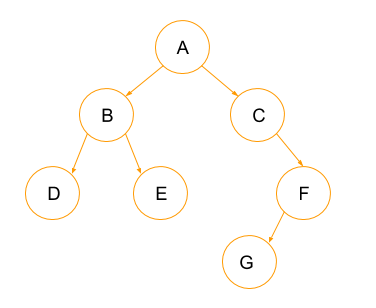
ساختارهای داده خطی، مانند آرایه ها یا لیست های پیوندی نامرتب، با افزایش اندازه داده ها دچار پیچیدگی های فراوانی می شوند. بنابراین یک ساختار غیر خطی، درخت مانند با ایجاد امکان دسترسی سریع به داده ها با استفاده از ساختار سلسله مراتبی از پیچیدگی می کاهد.
برای مثال فایل های سیستم خود را در نظر بگیرید. هر پوشه یک نام دارد و فایل های مرتبط و پوشه های بیشتری در داخل آن ذخیره می شود. هنگام جستجوی یک فایل، به احتمال زیاد به پوشه والد می روید و شروع به جستجوی عمیق تر در آنجا می کنید. یا به جای آن، می توانید بر اساس نام فایل/پوشه در ریشه جستجو کنید!

درخت باینری چیست؟
درخت باینری یک ساختار داده غیر خطی است که در آن یک گره می تواند دارای 0، 1 یا 2 گره باشد. هر گره در درخت باینری یا به عنوان گره والد یا به عنوان گره فرزند نامیده می شود. بالاترین گره درخت باینری به عنوان گره ریشه نامیده می شود. هر گره والد می تواند حداکثر 2 گره فرزند داشته باشد که گره فرزند سمت چپ و گره فرزند سمت راست می باشد. جستجو در این درخت به راحتی انجام نمی شود زیرا از هیچ ترتیبی برای چیدمان عناصر پیروی نمی کند.
کاربردهای عملی
1- جداول مسیریابی روترها
هدف اصلي مسيريابها ارسالبستهها به سمت مقصد نهايی است.يک مسيرياب برای انجام اين کار بايد با توجه به گرهمقصد هر بسته تصميم بگيرد که آن را از کدام پورت خروجی به سمت مقصد بعدی ارسال نمايد. اطلاعات لازم برای اين کاردر يک جدول به نام جدول مسيريابی قرار دارد. با ظهور مسيريابی فاقد کلاسبندی، بيتهای مربوط به شناسه ی شبکه میتواند هر تعداد از کل بيتهای آدرس را شامل شود.اين عدد برای هر مدخل مسيريابی در جدول مسيريابی ذخيره میشود.بنابراين در اين حالت جدول مسيريابی شامل چندين پيشوند با طولهای متفاوت است وبايد برای مسيريابی هر بسته، از بين تمام پيشوندهايی که با آدرس مقصد بسته مطابقت دارند، طولانیترين آنها انتخاب شود.اين به معنای يک جستجوی دوبعدی در جدول مسيريابی است)طول و مقدار(که همين امر،پياده سازی اين جستجو را مشکل می سازد
یکی از راه های موجود استفاده از یک در خت دودویی می باشد. یک درخت دودويی که با شروع از ريشه ی آن، در هر سطح، يک بيت از آدرس مقصد بسته بررسی میشود وبا توجه به مقدار آن بيت، جستجو به يکی از دو فرزند چپ يا راست منتقل میشود. اين حرکت تا جايی که نتوان ادامه داد انجام میشود. اگر در مسير جستجو يک نود حاوی پيشوندمشاهده کنيم، مقدار آنرا به عنوان طولانیتري تطبيق مشاهد شده تا به حال، به خاطرمیسپاريم. برای این مسیریابی الگوریتم های بهینه ای در مقالات منتشر شده است که در بهینه ترین آنها از درخت دودویی استفاده می شود.
2- درخت تصمیم
درختان باینری همچنین می توانند برای اهداف طبقه بندی(classification) استفاده شوند. درخت تصمیم یک الگوریتم یادگیری ماشین نظارت شده است. ساختار داده درختی باینری در اینجا برای شبیه سازی فرآیند تصمیم گیری استفاده می شود. درخت تصمیم معمولا با یک گره ریشه شروع می شود. گره های داخلی شرایط یا ویژگی های مجموعه داده هستند. شاخه ها قوانین تصمیم گیری هستند در حالی که گره های برگ نتایج تصمیم هستند. به عنوان مثال، فرض کنید می خواهیم سیب ها را طبقه بندی کنیم. درخت تصمیم برای این مشکل به صورت زیر خواهد بود:
3- ارزیابی عبارات
درخت بیان دودویی یک درخت باینری است که در آن عملگرها در گرههای داخلی درخت ذخیره میشوند و برگها دارای عملوندها هستند. فرض کنید هر گره از درخت عبارت باینری صفر یا دو فرزند دارد. عملگرهای پشتیبانی شده عبارتند از +(جمع)، −(تفریق)، *(ضرب)، ÷(تقسیم) و ^(توان).
به عنوان مثال، مقدار درخت عبارت زیر 28 است:

4- مرتب سازی
درختهای جستجوی دودویی، گونهای از درختهای باینری هستند که در الگوریتمهای مرتبسازی استفاده میشوند. درخت جستجوی دودویی به سادگی یک درخت باینری مرتب شده است به طوری که مقدار در فرزند سمت چپ کمتر از مقدار در گره والد است. در عین حال، مقادیر در گره سمت راست بیشتر از مقدار در گره والد است. برای تکمیل یک روش مرتب سازی، مواردی که باید مرتب شوند ابتدا در درخت جستجوی دودویی قرار می گیرند.
درخت جستجوی باینری یا دودویی
یک درخت دودویی شرایط خاصی دارد که در آن هر گره در حالت بیشینه دو فرزند دارد. یک درخت دودویی مزیتهای یک آرایه نامرتب و همچنین یک لیست پیوندی را با هم دارد. جستجوی درخت دودویی به اندازه آرایه مرتب سریع است و عملیاتهای درج و حذف نیز به اندازه لیست پیوندی سریع هستند.
شرایط یک درخت جستجوی دودویی
- زیردرخت سمت چپ یک نود حتما باید نودهایی با مقداری کمتر از والد داشته باشد.
- زیردرخت سمت راست یک نود حتما باید نودهایی با مقداری بیشتر از والد داشته باشد.
- هر یک از زیر درختهای چپ و راست نیز باید یک درخت جستجوی دودویی باشند.
- هیچ نودتکراری نباید وجود داشته باشد.
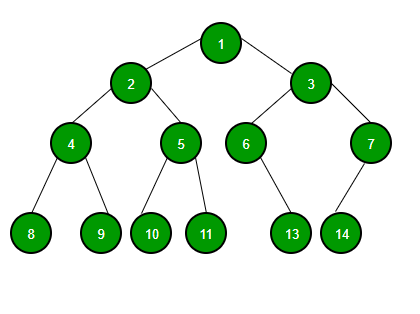
برای مثال مسیر جستجو در یک درخت دودویی را بررسی می کنیم:

در درخت بالا به دنبال عدد 6 می گردیم. عدد 6 را با ریشه مقایسه می کنیم از ریشه کوچکتر است پس طبیعتا به طرف زیردرخت چپ باید حرکت کنیم، سپس با عدد 3 مقایسه می شود عدد6 بزرگتر از 3 پس به سمت زیردرخت راست حرکت کرده و به عدد 6 میرسیم. 8 -> 3 -> 6
حال اگر در درخت بالا پیمایش بصورت (فرزندچپ – ریشه – فرزند راست) داشته باشیم اعداد ما مرتب شده اند. 1-3-4-6-7-8-10-13-14
5-شاخص سازی پایگاه داده
در نمایه سازی پایگاه داده، B-trees برای مرتب سازی داده ها برای جستجوی ساده، درج و حذف استفاده می شود. توجه به این نکته مهم است که درخت B یک درخت باینری نیست، اما می تواند تبدیل به یک درخت باینری شود. پایگاه داده برای هر رکورد موجود شاخص هایی ایجاد می کند. سپس B-tree در گره های داخلی خود، ارجاع رکوردهای داده با رکوردهای داده واقعی در گره های برگ خود ذخیره می کند. این امکان دسترسی متوالی به داده ها در پایگاه های داده را فراهم می کند.
DBMS ها از کارایی لگاریتمی نمایه سازی B-tree برای کاهش تعداد خواندن های مورد نیاز از دیسک برای یافتن یک رکورد خاص استفاده می کنند.
6- فشرده سازی داده ها
در فشرده سازی داده ها، کدگذاری هافمن برای ایجاد یک درخت باینری با قابلیت فشرده سازی داده ها استفاده می شود. فشرده سازی داده ها پردازش داده های رمزگذاری شده برای استفاده از فضای کمتر است.مانند مواردی که توسط فرمت های فایل .jpeg و .mp3 استفاده می شود.
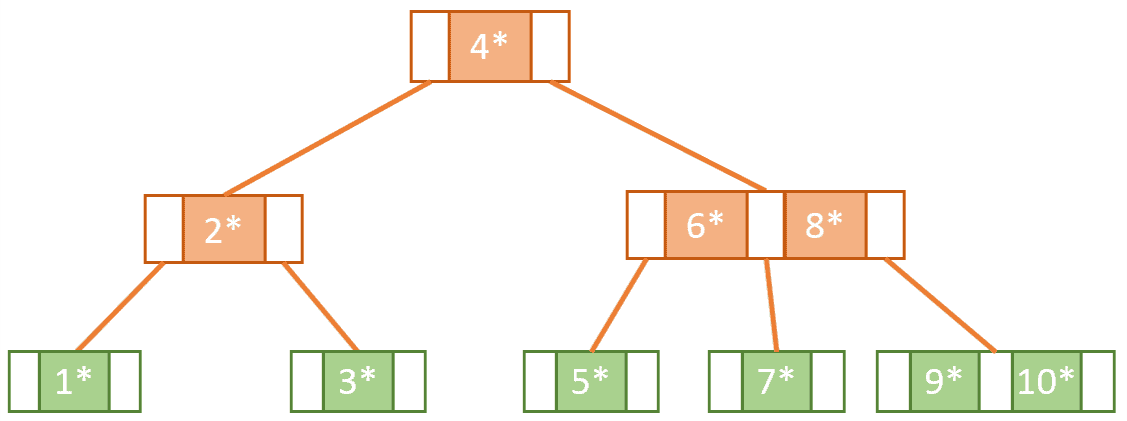
کدینگ هافمن با دادن متنی برای فشرده سازی، یک درخت دودویی می سازد و رمزگذاری کاراکترها را بر اساس تعداد تکرار آنها در متن درج می کند. رمزگذاری یک کاراکتر با پیمایش درخت از ریشه تا گره به دست می آید. کاراکترهایی که تکرار بیشتری داشته اند در مقایسه با کاراکترهای کمتر دارای مسیر کوتاهتری خواهند بود. این کار برای کاهش تعداد بیت ها برای کاراکترهای مکرر و اطمینان از حداکثر فشرده سازی داده ها انجام می شود.
روش هافمن :
-1 چگالی هر کاراکتر را محاسبه میکنیم (تعداد دفعات حضور کاراکتر در متن مورد نظر).
-2 دو کاراکتر با کمترین میزان تکرار (چگالی) را انتخاب میکنیم.
-3 کاراکتر های مرحله 2 را با کاراکتر جدیدی که دارای چگالی برابر با مجموع چگالی دو کاراکتر فوق است جایگزین میکنیم.
-4 تا زمانی که فقط یک کاراکتر باقی مانده باشد، به مرحله 2 میرویم.
-5 از عملیات فوق یک درخت حاصل می شود، بر روی این درخت هر مسیر به سمت چپ با 0 و هر مسیر به سمت راست با 1 وزن دهی میشود.
-6 کد هر کاراکتر با کنار هم گذاشتن وزن ها از ریشه تا آن کاراکتر به دست می آید.
مثال:
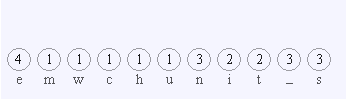
عددی که بالای هر کاراکتر نوشته شده است نشان دهنده تعداد دفعات تکرار آن کاراکتر در رشته مورد نظر است.
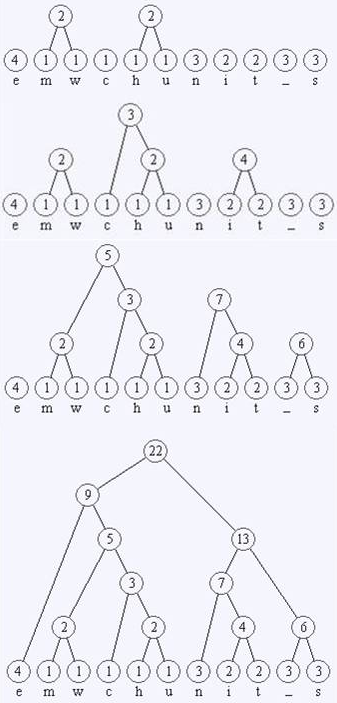
m,w,c,h,u کمترین تکرار را دارند؛ ما مجازیم هرکدام از دو زوجی که کمترین مقدار را دارند دو به دو در نظر بگیریم..پس از این مرحله چگالی ها = 3-3-2-2-3-2-1-2-4خواهد بود(اعداد پر رنگ جایگزین جدید هستند)
سپس چگالی ها 3-3-4-3-3-2-4خواهد شد و سپس چگالی ها 6–7–5-4خواهد شد. همینطور تا مرحله پایانی ادامه می دهیم، پس از اتمام این مرحله تنها عدد 22 باقی خواهد ماند و دیگر نمیتوانیم جفتی برای ادامه دادن الگوریتم پیدا کنیم.
سپس فرزند راست عدد 1 و فرزند چپ عدد صفر را قرار میدهیم و سپس عدد موجود بر یال هر کاراکتر را از ریشه تا آن کاراکتر میخوانیم.
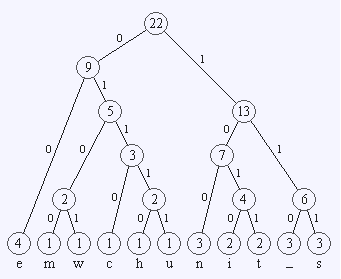
E: 00
M: 0100
W: 0101
C: 0110
H: 01110
U: 01111
N: 100
I: 1010
T: 1011
_: 110
S: 111
در این روش کاراکترهای پرکاربرد تر با رشتههای بیتی کوتاهتری نسبت به آنهایی که تکرارشان کمتر است، نشان داده میشوند. به حرف Eکه تعداد تکرار بیشتری داشته کد کوچکتر 00 اختصاص داده شده است.
7- تقسیم بندی فضای باینری(Binary Space Partition)
پارتیشن بندی فضای دودویی (BSP) روشی برای پارتیشن بندی فضا است که به صورت بازگشتی یک فضای اقلیدسی را با استفاده از ابرصفحه ها به عنوان پارتیشن به دو مجموعه محدب تقسیم می کند. این فرآیند تقسیم بندی، نمایشی از اشیاء درون فضا را در قالب یک ساختار داده درختی به نام درخت BSP ایجاد می کند و تقریباً در هر بازی ویدیویی سه بعدی برای تعیین اینکه چه اشیایی باید رندر شوند استفاده می شود.
پارتیشن بندی فضای دودویی در زمینه گرافیک کامپیوتری سه بعدی در سال 1969 توسعه یافت. ساختار یک درخت BSP در رندر مفید است زیرا می تواند به طور موثر اطلاعات مکانی در مورد اشیاء در یک صحنه ارائه دهد، مانند اشیایی که از جلو به عقب با توجه به یک بیننده در یک مکان مشخص مرتب می شوند. سایر کاربردهای BSP عبارتند از: انجام عملیات هندسی با اشکال (هندسه جامد سازنده) در CAD، تشخیص برخورد در رباتیک و بازی های ویدئویی سه بعدی، ردیابی پرتوها و سایر برنامه هایی که شامل مدیریت صحنه های فضایی پیچیده است.

درخت BSP داده های عددی را ذخیره می کند، نه یک قالب گرافیکی که در اینجا نشان داده ایم. خود داده ها در یک جدول یا پایگاه داده ذخیره می شوند. نمودار درختی BSP فقط ابزاری است که توسعه دهندگان از آن برای تجسم داده ها استفاده می کنند. در گرافیک کامپیوتری، یک تصویر به صورت مجموعه ای از سه یا چهار نقطه (راس) در فضای سه بعدی ذخیره می شود. هنگامی که “نقطه ها را به هم وصل می کنید”، چهره ای با سه رأس دریافت می کنید. مجموعه نقاط آن چیزی است که در یک ساختار داده BSP ذخیره می شود.
8- درخت هش و ارزهای دیجیتال
همانطور که میدانید در بلاک چین هر تراکنش شناسهی مخصوص خود را دارد. در بیشتر بلاک چینها این شناسه یک رشته کد ۶۴ کاراکتری است که ۲۵۶ بیت (یا همان ۳۲ بایت) از حافظه را اشغال میکند. حال وقتی به این موضوع فکر کنید که بلاک چینها از صدها هزار بلاک تشکیل شدهاند که هر بلاک خودش چندین هزار تراکنش را در خود جای میدهد، کاملاً برایتان مشخص میشود که موضوع حافظه و قدرت پردازشی دو مشکل عمدهی این فناوری هستند. بنابراین بهترین کار این است که تا میتوانیم از دادههای کمتری برای پردازش و تأیید تراکنشها استفاده کنیم که عمدتا این کار را با عملیات رمزگذاری و تابع هش(هش (Hash) تابعی است که ورودیهایی از اعداد و حروف را پذیرفته و آنها را به یک خروجی رمزگذاری شده با طولی یکسان تبدیل میکند. هشها با استفاده از یک الگوریتم ساخته میشوند و برای مدیریت بلاک چین در یک رمز ارز ضروری میباشند. نکته مهم در توابع هش این است که نمیتوانیم با داشتن خروجی به ورودی برسیم.) انجام میدهند.

درخت مرکل چیست؟
درخت مرکل درواقع درختی است که ساختار داده را نمایش میدهد. در این روش هر «گره غیربرگ» یک هش را در خود ذخیره میکند که از روی دادههای گرههای زیرین خود تولید شده است.
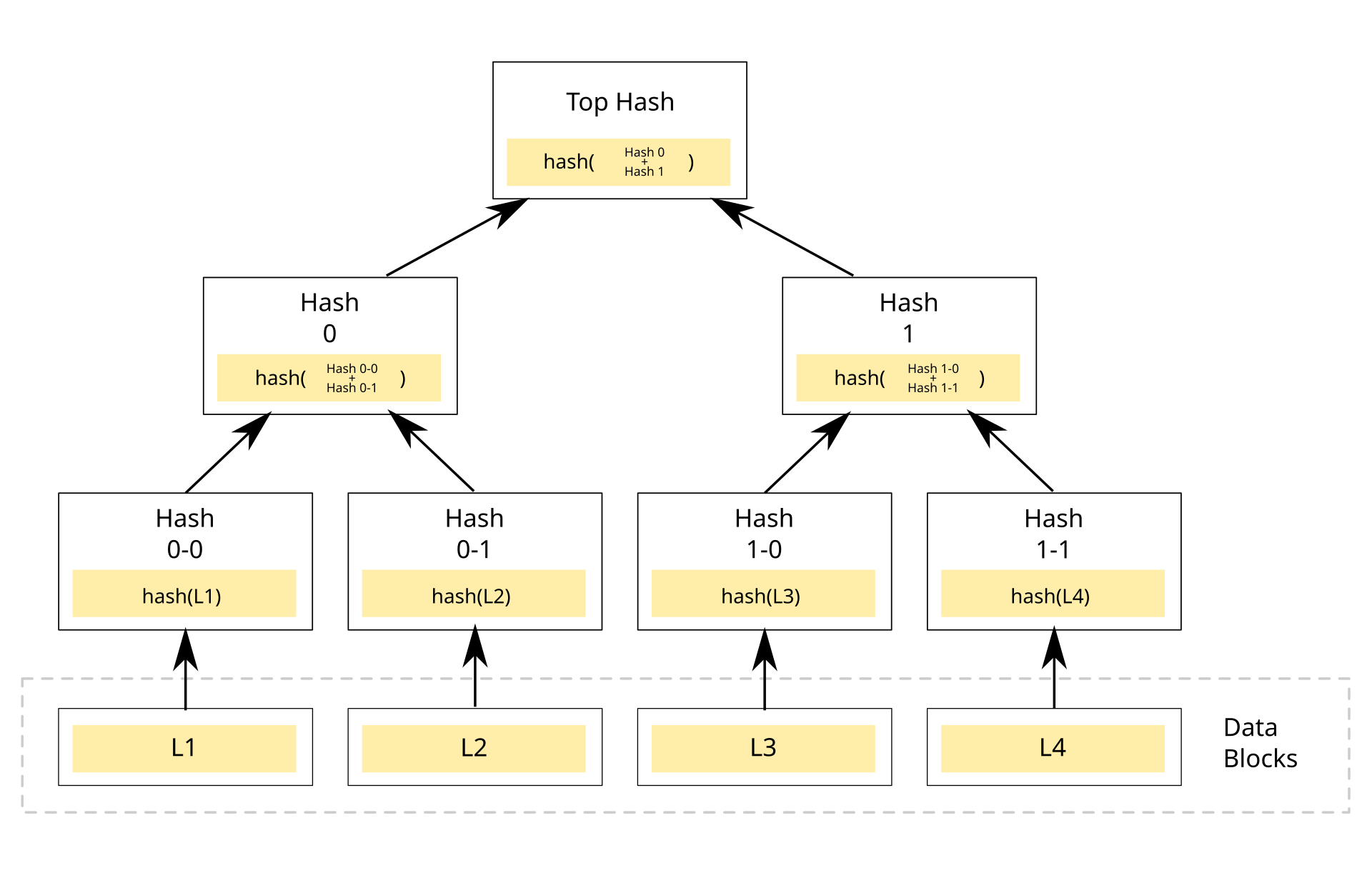
بنابراین هر درخت مرکل میتواند به تنهایی یک تراکنش را در خود خلاصه کند. از آنجایی که گفتیم در توابع هش با تغییر یک کاراکتر از ورودی، خروجی به کل تغییر میکند، به همین دلیل تنها با داشتن ریشهی درخت مرکل که حاوی یک هش است، میتوان از درستی گرههای برگ و محتوای آنها اطمینان حاصل کرد. زیرا اگر تغییری در هر کدام از گرهها اتفاق بیفتد، هش ریشهی درخت مرکل هم بهکلی عوض میشود.
کاربرد درخت مرکل در بیت کوین
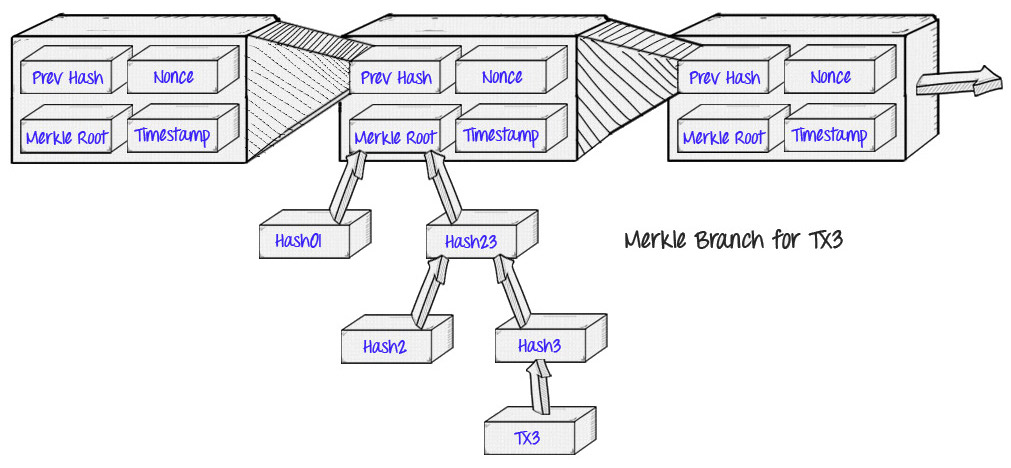
تابع هشی که بیت کوین از آن استفاده میکند SHA-256 نام دارد. خروجی این الگوریتم همواره یک رشته کاراکتر ۲۵۶ بیتی است. همانطور میدانید بلاکهای هر بلاک چین با داشتن هش بلاک قبلی خود به یکدیگر متصل هستند.
تراکنشهای صورتگرفته در شبکهی بیت کوین توسط ماینرها به داخل بلاک افزوده میشوند و بعد از هشگذاری درخت مرکل، در نهایت هش ریشهای که به دست میآید در سرتیتر بلاک در کنار موارد دیگر نوشته میشود. بدین ترتیب لازم نیست که کل اطلاعات تراکنش به شکل کامل در بلاک ذخیره شوند. زیرا با داشتن هش ریشهی درخت مرکل میتوان درستی تراکنشهای قبلی را تأیید کرد و فضای کمتری نیز اشغال می شود.
9- درخت هیپ
هیپ حالت خاصی از ساختمان داده درخت باینری متعادل است که در آن کلید ریشه-گره با فرزندانش مقایسه شده و بر همین اساس مرتب میشود.
Min-Heap – که مقدار گره ریشه کمتر یا مساوی یکی از فرزندانش باشد.
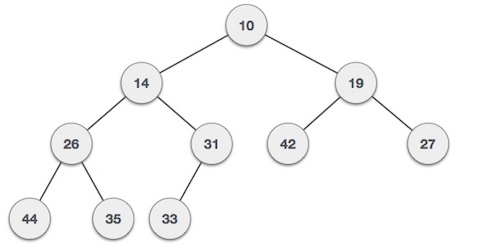
Max-Heap – که مقدار گره ریشه بزرگتر یا مساوی یکی از فرزندانش است.
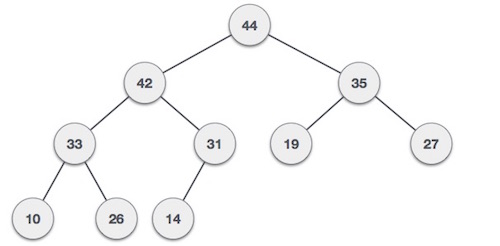
- مرتبسازی هرمی: یکی از بهترین شیوههای مرتبسازی است که «درجا» (in place) انجام میشود و در بدترین حالت نیز مرتبه زمانی خطی دارد.
- الگوریتم انتخاب: برای یافتن عنصر بیشینه، کمینه، میانه و kامین عنصر در زمان خطی به کار میرود.
- الگوریتمهای گراف: با استفاده از هرم به عنوان زمان بهینهٔ پیمایش، زمان اجرا به صورت چند جملهای کاهش مییابد. این الگوریتمها برای مواردی مانند الگوریتم پریم و الگوریتم دیکسترا استفاده میشوند.
- صف اولویت دار: برای پیادهسازی صف اولویت دار معمولاً از هرم کمینه استفاده میشود.
10- درخت GGM
در برنامه های رمزنگاری برای تولید درختی از اعداد شبه تصادفی استفاده می شود.

اگر این مقاله برای شما مفید بود است حتما نظرات خود را با ما در میان بگذارید.
تمامی حقوق برای ماکرونت محفوظ است.